Experiment A: “Lithic Economies: Molloy’s Sucking Stones”
Introduction
In opening his stone-soliloquy, Molloy explains that he “took advantage of being at the seaside to lay in a store of sucking-stones.”1 The number of stones is sixteen, and Molloy would prefer to suck on these stones systematically, so that their erosion proceeds evenly. For convenience, Molloy plans to carry the stones in one or all of his pockets; he has two trouser pockets and two greatcoat pockets, making a total of four pockets. Molloy’s problem (and our own) will be to devise a method of distribution and circulation of the stones that ensures each stone will pass through Molloy’s mouth at least once and no more than once before a new cycle of sucking begins. This system should be simple in the extreme—possible to execute without thought—as Molloy cannot be bothered to keep track of an elaborately devised plan.
Hypothesis
The sucking stone, being a fictional entity, is for this reason no less ideal an object for sucking. The sucking stone may be an (post)allegorical pebble, but will neither be more nor less material for this reason. However, if an emblem, it will prove mutable and, thus, difficult to suck in any systematic way.
Materials
16 stones
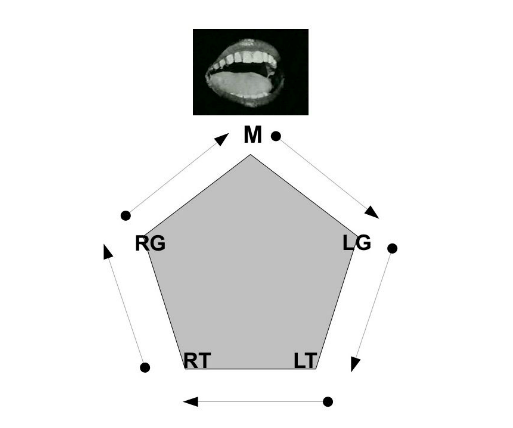
1 pair trousers with two pockets, Left Trouser (LT) and Right Trouser (RT)
1 greatcoat with two pockets, Left Greatcoat (LG) and Right Greatcoat (RG)
1 mouth, for sucking (M)
Methods
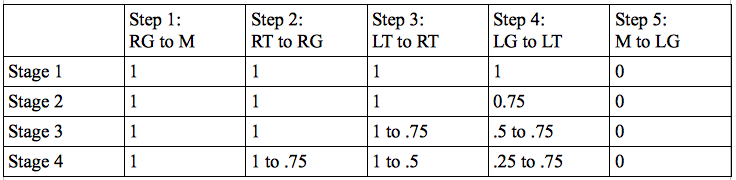
Method A. Molloy first plans to distribute the stones evenly amongst his four pockets, moving them one-at-a-time, beginning with a stone from RG which he moves to M (Step 1). While sucking this stone, the deficit in RG is made up by a stone from RT (Step 2). He then fills the deficit in RT with a stone from LT (Step 3), and the deficit in LT with a stone from LG (Step 4), thereby leaving LG with three stones, ready to receive the stone from M (Step 5) so that the cycle may begin again. The problem is that in the third step of the new cycle (the 2nd movement of a stone from LG to LT) Molloy cannot be sure he moves an unsucked stone. In fact, there is a one-in-four chance that the stone moved from LG to LT has already been sucked. In the following cycles, the probability of moving a sucked stone in step 4 increases exponentially and incrementally spreads to Steps 3, 2, and 1. See Table, “Method A,” below.
Method B. Molloy then considers moving all four stones as a group from one pocket to the next, so that beginning with the same Step 1 (RG to M) he would then move four stones from RT to RG (Step 2), four stones from LT to RT (Step 3), four stones from LG to LT (Step 4) and the three stones from RG plus the one sucked stone from M to LG (Step 5). Molloy quickly realizes this method presents the same problems as Method A, and concludes that the only sure solution would be to have sixteen pockets—a pocket for each stone. (A merely hypothetical solution as Molloy lacks both needle and thread, and the initiative).
Method C. In a moment of sudden illumination, Molloy realizes the dilemma is false and depends only upon his thinking symmetrically. If the stones are unbalanced to begin—so that six stones begin in RG, five in RT, five in LT and none in LG—and if the stones then move one-at-a-time from RG to M and from M to LG until RG is emptied, and if when RG empties out Molloy then moves the five stones from RT to RG, from LT to RT, and from LG to LT, and begins again with the transfer from RG to M to LG, then he will eventually complete one full cycle wherein each of the sixteen stones have been sucked exactly once—no more, no less.
Data
See: “Figures and Graphs,” below.
Results
The solution is “inelegant assuredly, but sound, sound.”2 The inelegance of this solution, however, results in a physical disequilibrium, so that Molloy confesses “it was something more than a principle I abandoned, when I abandoned the equal distribution, it was a bodily need.”3 A further confession reveals that Molloy could care less about being off-balance; the point of collecting sixteen stones “was not in order to ballast myself in such and such a way… but simply to have a little store, so as never to be without.”4 But then, Molloy’s next reflection reveals that he cares not for larding these stones for the future, and finally, he throws all but one away, which he eventually misplaces, ingests, or abandons.
Conclusion
In Molloy’s sucking-stone economy, uneven distribution is key to smooth circulation, but then aesthetics take precedence over utility, and ultimately, both are sacrificed to ambivalence. Molloy refuses to let the pebbles pile up in one pocket; he opposes dispersal to sedimentation. Disburthening is not asceticism in Molloy but minimalism, noise—an intentional interference with systems of desire and communication. At first Molloy acquires many stones, then he abandons them all through willful dispossession and ambivalence. Beckett similarly abandoned, at times, his native language—as if one stone were as good as another and none better than any.
Figures and Graphs
Method A. This graph charts the probability of moving an unsucked stone from one pocket to the next in each step of the four stages of one full cycle (which would consist of sixteen stages), where 1 represents a 100 percent probability of moving an unsucked stone and 0 a zero percent probability.